What is the most bizarre real number that you can imagine? Probably many people think of an irrational number such as pi (π) or Euler’s number. And indeed, such values can be considered “wild.” After all, their decimal representation is infinite, with no digits ever repeating. Even such bonkers-looking numbers, however, together with all the rational numbers, make up only a tiny fraction of the real numbers, or numbers that can appear along a number line. (As a reminder, these are the kinds of numbers that can be used in all manner of familiar measurements, including time, temperature and distance.)

But it turns out that if you happened to pick out a number at random on a number line, you would almost certainly draw a “noncomputable” number. For such values, there is no way to determine them precisely.

The real numbers are made up of the rational and irrational numbers. The rational numbers (that is, numbers that can be written as the fraction ^p⁄_q, where p and q are integers) include the natural numbers (0, 1, 2, 3,…) and the integers (…, –2, –1, 0, 1, 2,…). The rest of the numbers on the number line are irrational numbers. These, too, can be divided into different categories—most of which we can’t even imagine.

That infinities, infinitesimals, imaginary numbers or other unusual number spaces can be difficult to describe may not seem too surprising. But one would think we could fully understand the real numbers that describe distances in our world by now. Unfortunately, it is not that simple. To understand this, we must take a closer look at the irrational numbers.

What Numbers Are Irrationals?

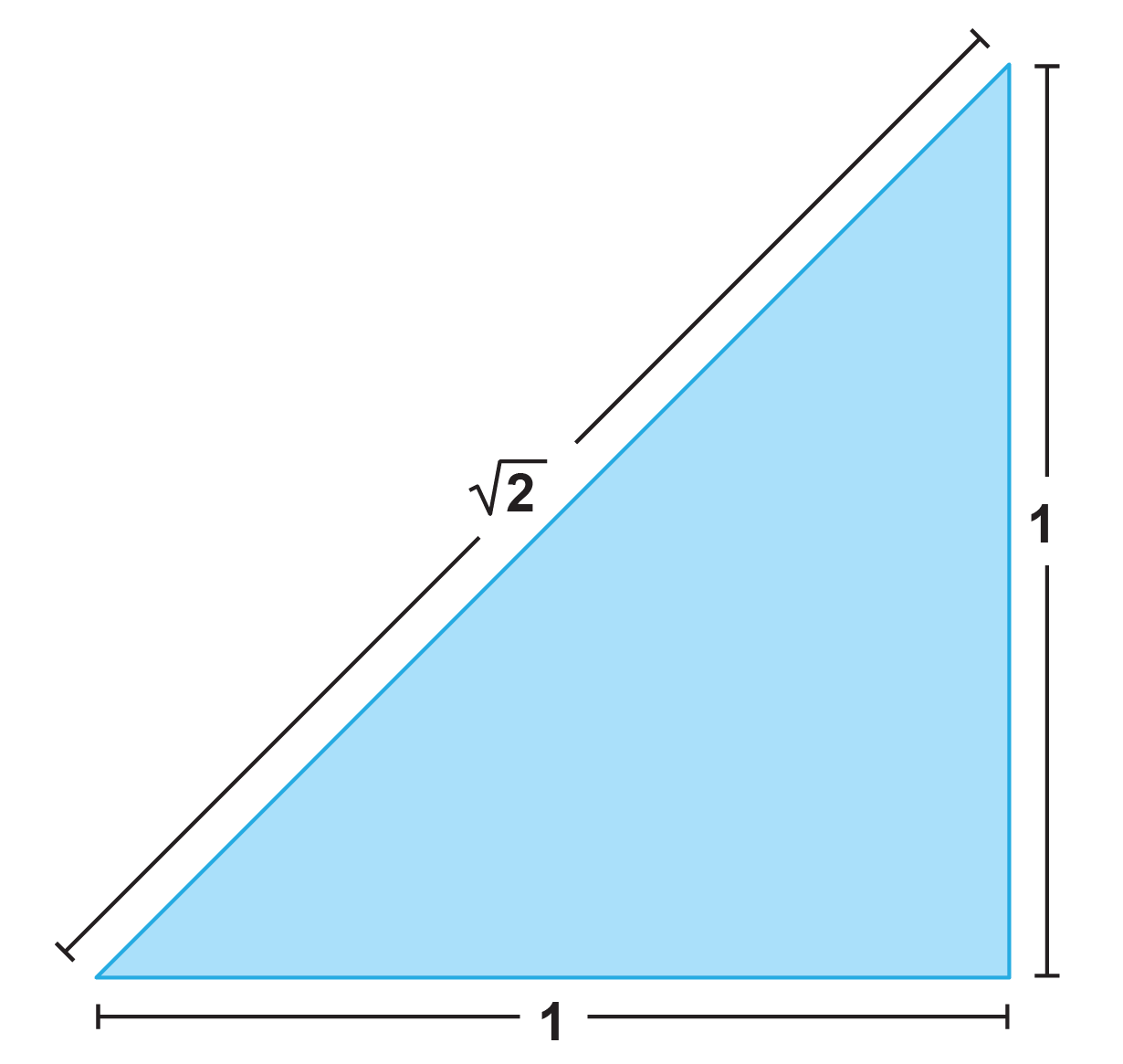
All real numbers that cannot be represented by a fraction of two integers are irrational. (Reminder: an integer is a whole number.) Irrational numbers include, for example, the square root of 2, whose decimal representation is infinite without ever repeating. In fact, √2 is among the simplest irrational numbers because it is constructible—that is, it can be generated with a compass and ruler by drawing a right triangle with two sides that have a length of one unit. The hypotenuse of that triangle then has the length √2. In a similar way, the golden ratio φ can be constructed geometrically, as can many other irrational values.

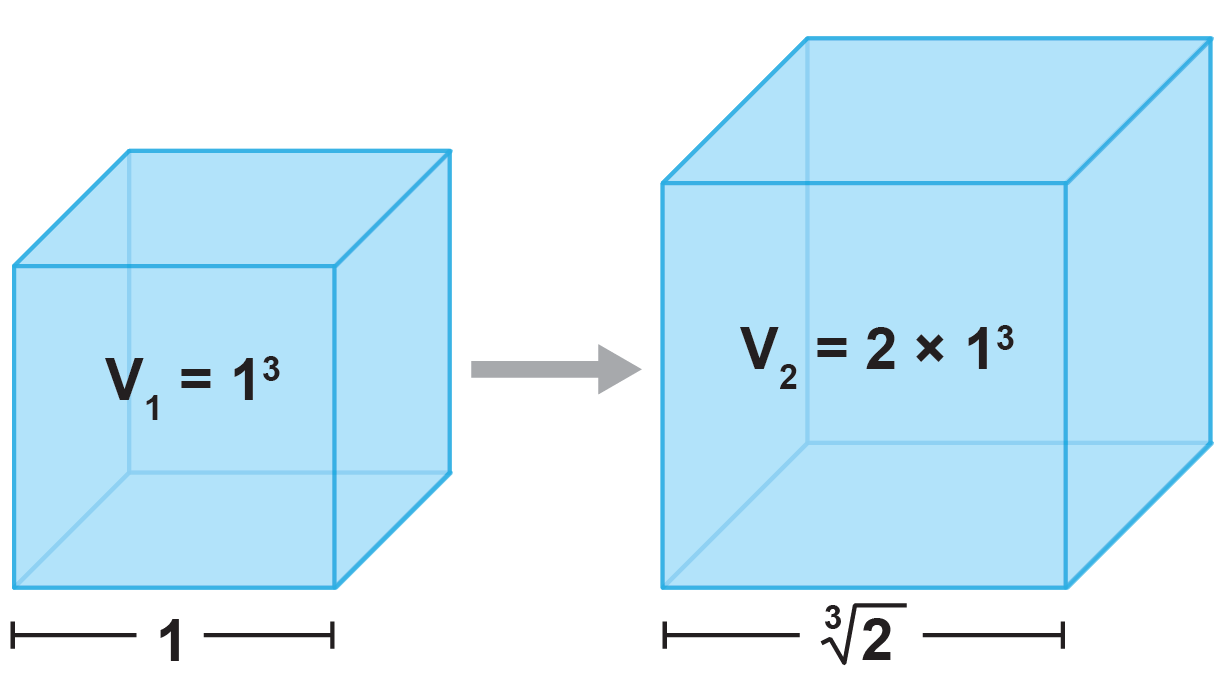
Even in ancient times, however, people encountered numbers that could no longer be generated in such a simple geometric way. A famous example is the doubling of a cube: How can a cube with a side length of 1 be constructed into a cube with twice the volume? As mathematician Pierre Wantzel found out in 1837, the edge length ∛2 required for this new cube cannot be constructed using a compass and ruler. But ∛2 belongs to the algebraic numbers, which can be written as solution of a polynomial equation. For ∛2, a corresponding equation is x³ = 2.

Some Numbers Are Transcendental

There are also transcendental numbers, which cannot be expressed as a solution of such equations. That is, there is no simple formula with which they can be calculated. Famously, π falls into this category. But that doesn’t mean that we don’t know its value. Greek mathematician Archimedes found a  calculation rule to determine π, at least approximately. In addition, there are  numerous algorithms that spit out the 587 millionth decimal place of π at will. With enough computing power and time, the number can be determined with arbitrary accuracy, at least in theory. The same applies to Euler’s number (e), or 2^√2.

The transcendental numbers hold several mysteries. While there are clear methods to tell whether a number is constructible, by contrast, it is difficult to prove whether a value is transcendental. For example, in 1934  Soviet mathematician Alexander Gelfond was able to prove that the composite number e^π is transcendental. But whether the values π^e or π x e or π – e are algebraic or transcendental is still unclear today.

Noncomputable Numbers Are Even Stranger

Until the early 20th century, people assumed that transcendental numbers were the wildest thing that real numbers had to offer. But that was wrong. In 1937 British mathematician Alan Turing published a paper on computable numbers. He used this term to describe all those values for which there is a calculation rule (that is, an algorithm) that a computer can perform to calculate the numerical value with any degree of accuracy.

Almost all known transcendental numbers, such as π and e, fall into this category. After all, we know their at least approximate numerical value and also how they can be calculated. As Turing showed in his work, however, equally noncomputable numbers exist whose values cannot be approximated with arbitrary precision—that is, we have no idea what they look like.

Even worse: almost all real numbers are not computable.

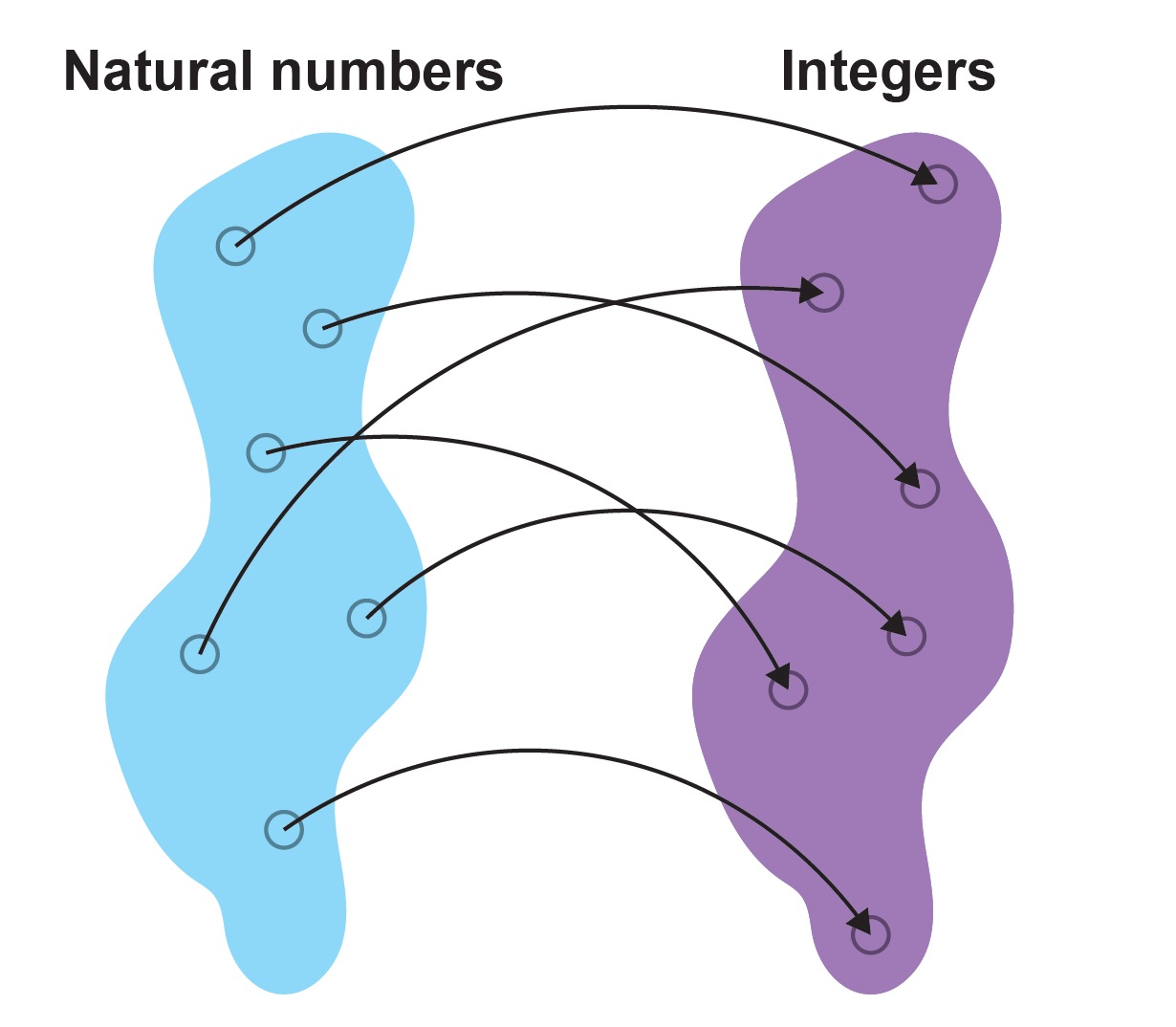
One recognizes this if one thinks about the infinite sizes of the different number sets. Mathematician Georg Cantor laid the foundations for this idea at the end of the 19th century. At that time, he was able to show, for example, that the set of natural, integer and rational numbers have the same cardinality (a mathematical expression for the size of a set). How so? To understand, one should first note that the same rules of calculation for finite numbers do not apply to infinities. Take, for example, the natural numbers and the integers: one can alternately assign a positive and a negative integer to each natural number, say (0, 0), (1, –1), (2, 1), (3, –2), (4, 2), and so on. Because there is no end to the natural numbers, we have thus found a one-to-one mapping between the two sets. It’s like assigning exactly one seat on the bus to each person at a bus stop, and vice versa. In this case, we know that there are as many seats on the bus as there are people at the bus stop. It is the same with the natural numbers and the integers.

A similar one-to-one mapping can be found between the rational and natural numbers. As Cantor was able to show, the cardinality of the natural numbers is the smallest possible infinity. He called it “countably infinite.”

The real numbers, on the other hand, cannot be counted. Cantor was able to prove  that the cardinality of the real numbers is necessarily greater than that of the natural ones. He did this by demonstrating that there is no way to enumerate all the real numbers in a list (however long it may be) without omitting some values. Thus, the real numbers form an uncountable set.

Cantor’s reasoning went as follows: Suppose one has a list of all the real numbers. Then one can imagine this list as a table. In each row, there is a number, with each column offering a position for a decimal place. Cantor demonstrated that if you draw a circle around a set of numbers forming a diagonal across this table (such as the first digit in the first row, second digit in the second row, etcetera), you can create a new real number by adding 1 to each diagonal entry. This new number cannot be contained in the list. Thus, your original list of all real numbers is incomplete.

But as Turing stated, all computable numbers must be countable. For each of these numbers, one can develop a machine that simply computes its value. Because one can number these calculating machines, the computable numbers are necessarily countable. This in turn has the consequence of the noncomputable numbers making up the majority of real numbers by far: there is an uncountable number of them!

So if you calculate the probability of what kind of real number you will encounter if you randomly draw one, you will get a clear result: in 100 percent of the cases, this number will not be computable. But that doesn’t mean you can’t draw any other number. With an infinite set of events, a probability of zero doesn’t mean an outcome is impossible.

The fact that noncomputable numbers are so abundant is all the more surprising, given that not many of these numbers are known.

The Halting Problem as Inspiration

The few existing examples of noncomputable numbers were defined by the famous halting problem from computer science. To think about this problem, developed by Turing, imagine a computer executing a specific set of instructions in order to solve a problem (in other words, the computer is using an algorithm). In the halting problem, you are asked to imagine a machine that could judge whether a computer running a given algorithm will stop at some point or continue forever. As Turing proved, while such a machine could judge whether some algorithms can be executed in finite time, there is demonstrably no method that can do this for all possible program codes. The halting problem is a direct application of mathematician Kurt Gödel’s incompleteness theorems, which state that not all mathematical statements can be proved.

The halting problem was used by Argentine-American mathematician Gregory Chaitin to define a noncomputable number. The so-called Chaitin constant Ω corresponds to the probability with which the theoretical model of a computer (a Turing machine) stops for any given input: Ω = –∑_p½^|p|, where p denotes all programs that halt after a finite runtime and |p| describes the length of the program in units of bits.

Thus, to compute the Chaitin constant exactly, one would need to know which programs halt and which do not, which is not possible, according to the halting problem. Nevertheless, in 2000  mathematician Cristian S. Calude and his colleagues succeeded in calculating the first digits of the Chaitin constant: 0.0157499939956247687….

This means that if you randomly generate a program in a language that Calude and his colleagues used, it will hold with a probability of about 1.58 percent in a finite run time. Even if the result has a high accuracy, the Chaitin constant cannot be calculated with arbitrary precision.

A Noncomputable Number and a Busy Beaver

Another noncomputable number results from the “busy beaver function,” or BB(n). This function computes the largest possible output (measured in bits) that an algorithm can produce from n bits.

For example, a noncomputable number results from the following construction: ∑_n½^BB(n). So far, only the first four values of the busy beaver function are known. Two other values can, at least, be estimated.

Thus, the first digits of this noncomputable number are ∑_n½^BB(n) = 0.51562548….

There are other complicated methods for defining noncomputable numbers. Perhaps you can come up with a variation as well. Still, given the abundance of computable numbers we know, it is always surprising that noncomputable values dominate the real numbers—and thus our world.

This article originally appeared in Spektrum der Wissenschaft and was reproduced with permission.